Hello, Time!

Catalogue

1. 1. Sequential Logic (Unit 3.1)
   1. 1.1. Clock (Integer Time Unit)
   2. 1.2. Combinatorial Logic Vs. Sequential Logic
2. 2. Flip Flops(触发器) (Unit 3.2)
   1. 2.1. D Flip Flop
   2. 2.2. How to build the D Flip Flop?
   3. 2.3. Remember Forever
3. 3. 1-Bit Register

Sequential Logic (Unit 3.1)

In this unit we introduce the issue of time into the system, since we didn’t have the notion of change before. To simplify the concept, we divide time into atomic pieces, which is clock.

Clock (Integer Time Unit)

Clock can be viewed as an oscillator at a certain fixed rate, of which each cycle is treated as a time unit, like time 0, time 1 and so on.

The signals are viewed as a indivisible thing as if nothing changes within each time unit. As a input signal is renewed every cycle, the output signal instantaneously follows (几乎同时).

You may wonder if this is real. Indeed, there may be delay in physical electrical signals. But, we can think it as a way that the voltage change (the grey area in the screenshot below) happens between cycles, while luckily, the cycles are a little bit wider than this instability. So, it is safe to ignore it and focus on the end of each time unit.

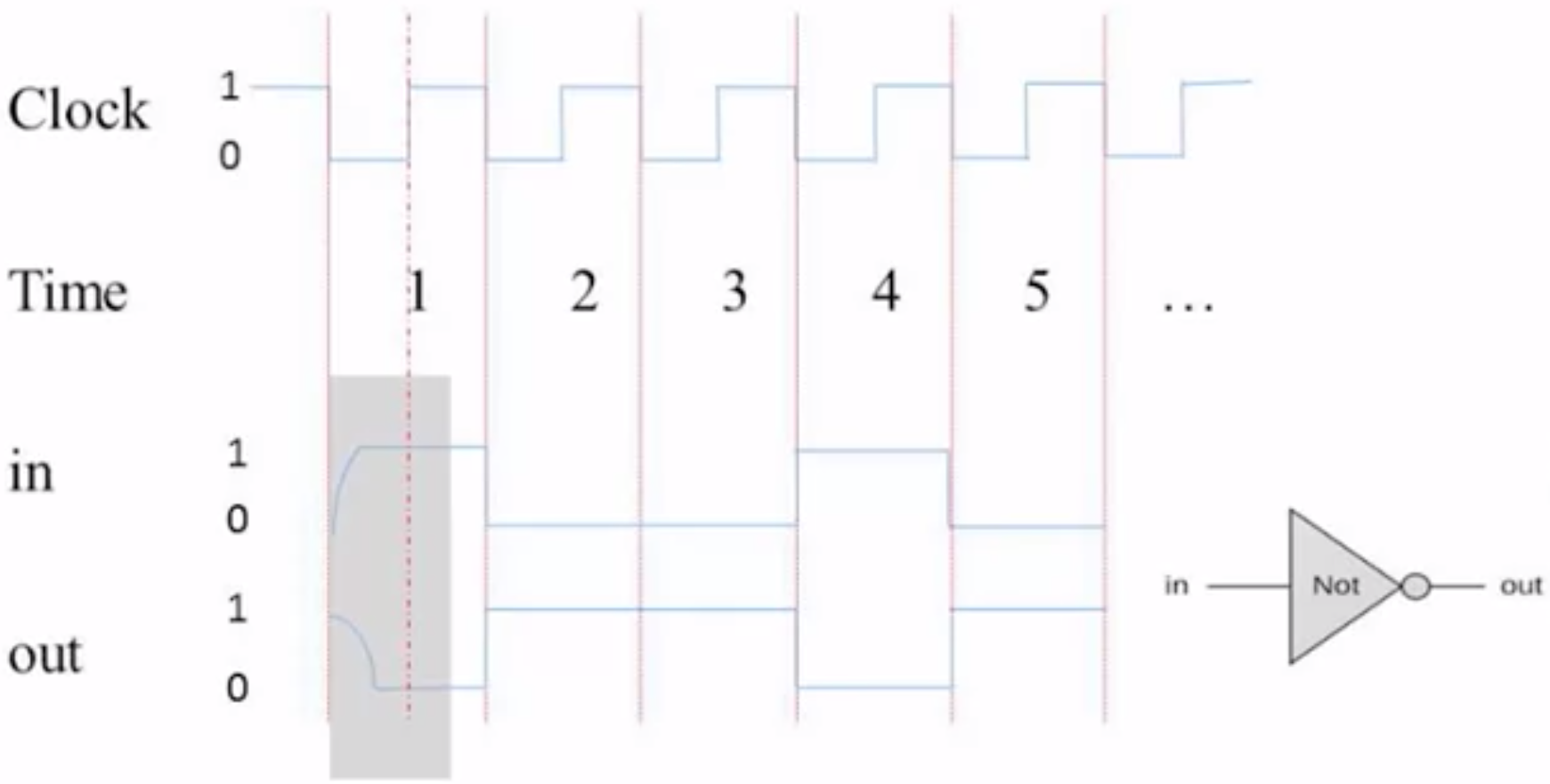
Also, (my guess) another reason may be given by the answer “Why binary?”. —> it may takes time to reach the final and consistent stage but not necessarily precise but it’s already enough to tell zero from one.

Combinatorial Logic Vs. Sequential Logic

Combinatorial:
$$
out[t] = function(in[t])
$$
Above is what we learned in the previous units.

Sequential:
$$
out[t] = function(in[t - 1])
$$
This is what we are going to talk about next.

---

The above topic requires an element: Remembering State, so that the time unit t can response according to time unit t - 1.

That means it has to be in two different physical states, which must be able to shift according to the logic of the previous time unit.

Flip Flops(触发器) (Unit 3.2)

Gates that can flip between 2 gates —> Flip Flops

D Flip Flop

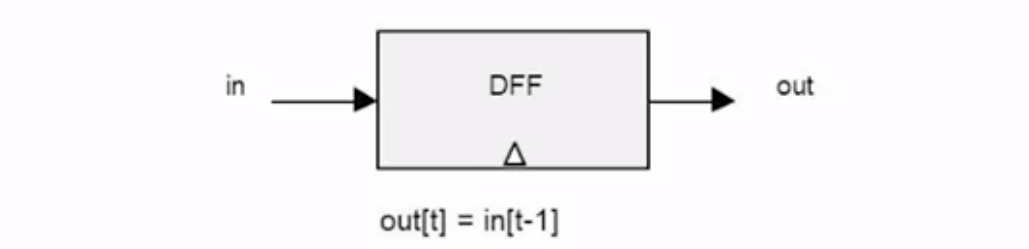
• The little triangle represents this is a sequential chip.
• It is primitive in this course, like Nand Gate, the base of all other gates.
• It can be built from Nand Gate.
• It is a simple gate with “memory”.

How to build the D Flip Flop?

Steps:

1. Create a loop which amplifying the same signal.
2. Provide isolation between sequential time units.
3. 再多的实现部分也不会在这个课上讲了……

Remember Forever

把D触发器输出连回到输入，就能实现数据的维持了。在回去的时候通过一些Combinatorial Logic就能进行其他计算的操作了。

这个可以进一步整合成一个“register”。

---

1-Bit Register

if (load(t - 1) == true)
	out(t) = in(t - 1) // Load in 
else
	out(t) = out(t - 1) // maintain

---

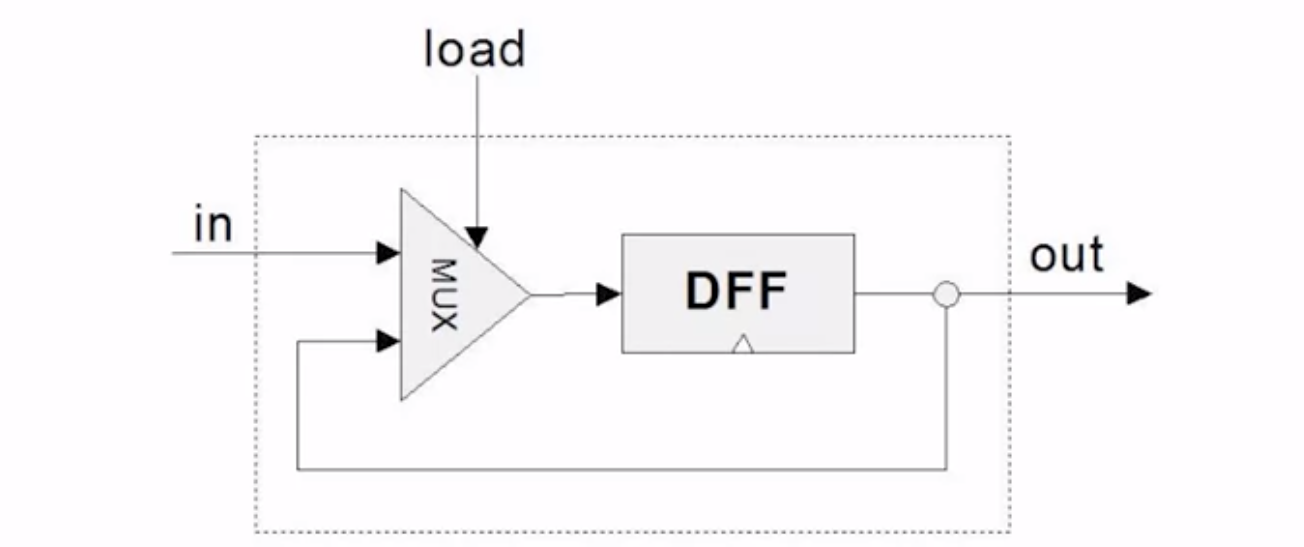
Once we work out the 1-bit memory, we can build the much larger memory.