Adding two numbers in binary representation is pretty simple. Here we are gonna build an Adder for binary numbers.
Starter (Unit 2.2)
Why does the Adder matter most?
Adder + Negative representation = Subtraction
Multiplication and Division are not hardware’s work, but software’s.
Three steps to build an Adder
- Half Adder: adds 2 bits
- Full Adder: adds 3 bits (used in “carry a 1”)
- Adder: adds 2 numbers
Half Adder: adds 2 bits
When we focus on a single slice of bits adding, like “1 + 1”, it has 2 outputs: a carry bit “1” and a result bit “0”.
| a | b | sum(Xor) | carry(And) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
CHIP HalfAdder is the first thing we need to implement in Project 2.
Full Adder: adds 3 bits
The last Half Adder is only for the case when carry is “0”, while Full Adder includes adding the carry and 2 bits together.
| a | b | c | sum | carry |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Tip: A Full Adder can be built with 2 Half Adders.
Adder: adds 2 numbers
Assuming the numbers are 16-bit long, we can implement it by connecting 16 Full Adders or 15 Full Adders and 1 Half Adder for the right-most bits.
Tips:
- The carry bit is “piped” up the significance ladder, from right to left.
- The MSB carry bit should be ignored.
Negative Numbers
2’s complement is elegant, and it enables us to do subtraction (negative addition) exactly the same way as addition.
Computing “-x”
By solving this, we can deal with subtraction! So, no more hardware needed for it!~
$$
-x = 2^n-x = 1 + (2^n - 1) - x
$$
Why converting this way?
Because $(2^n-1) $ is “all ones”, which makes subtraction very easy (no need to borrow anything!). —> JUST FLIP THE BITS of $x$
Then, add one. —> easy.
Negation steps in one word:
- Flip all the bits;
- Add one.
ALU (Unit 2.4)
Where is ALU? Let’s take a close look into the computer:
Von Neumann Architecture
$$
Computer System = Input + Memory + (Control + ALU) + Output
$$
In which,
$$
Control + ALU = CPU (Central Processing Unit)
$$
The Hack ALU
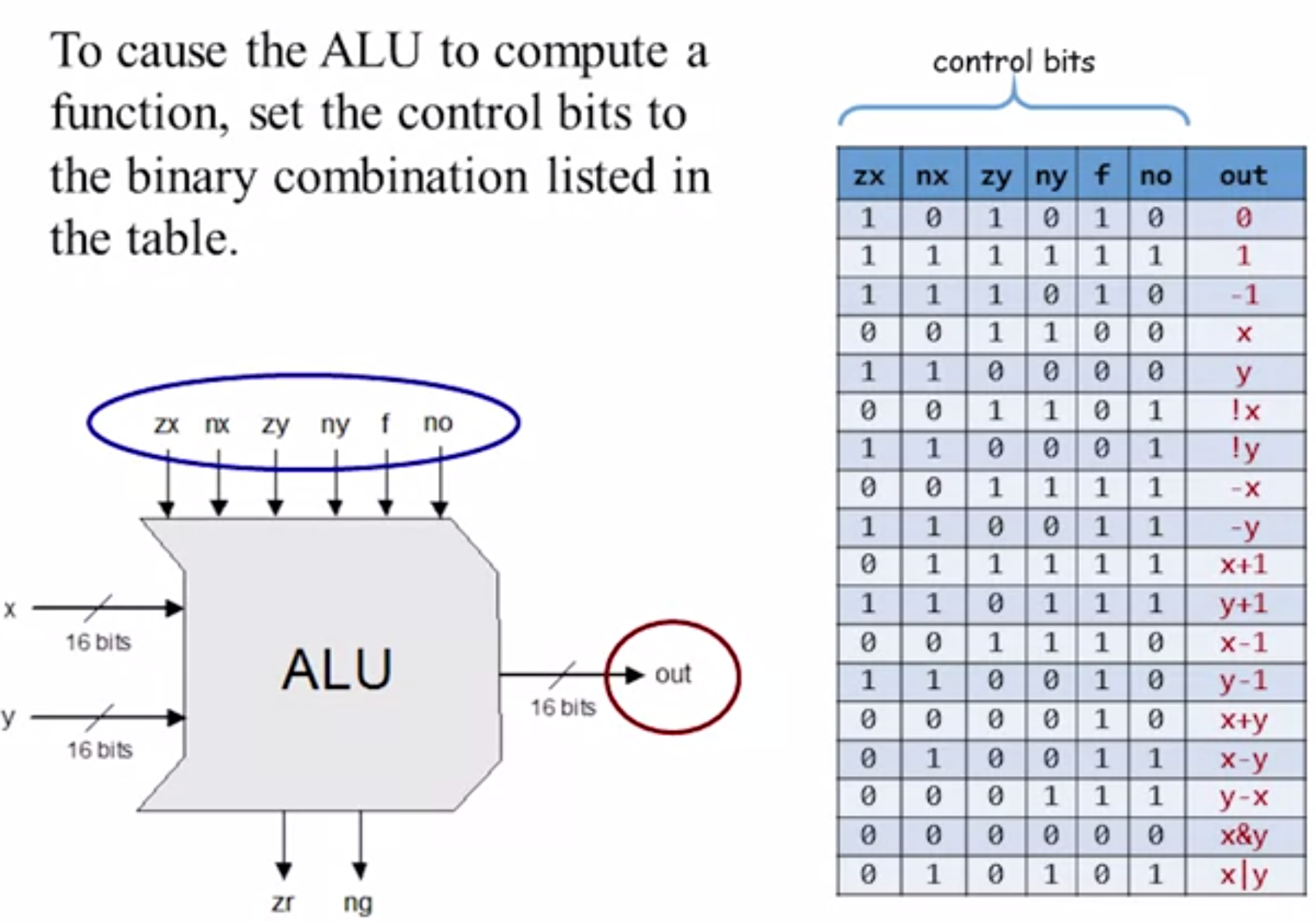
The 6 control bits represent which function to compute. zr and ng will be clear later.
Open the ALU Black Box
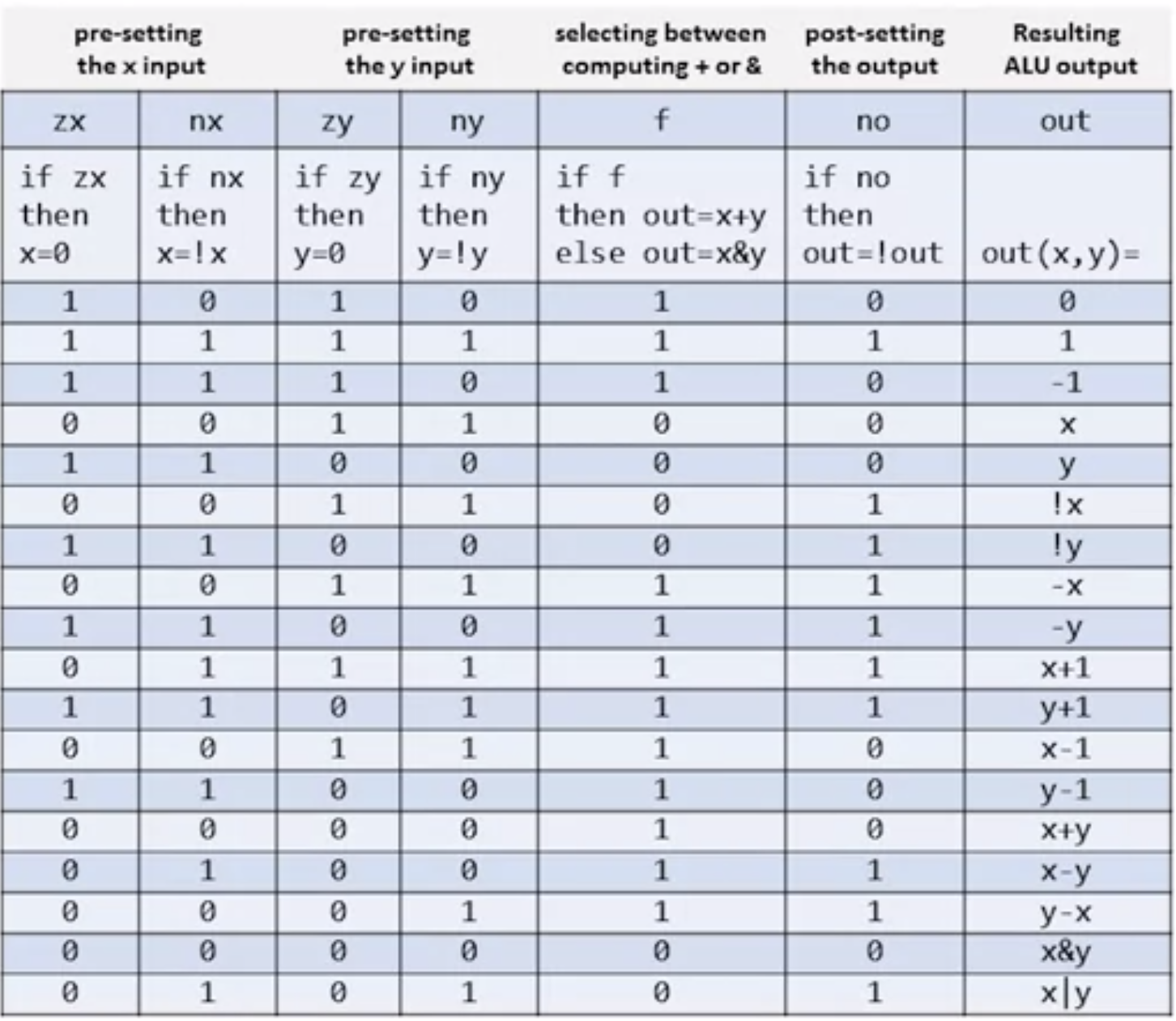
Control bits (blue circle in the last image):
zxif (zx) then x = 0nxif (nx) then x = !xzyif (zy) then y = 0nyif (zy) then y = !yfif (f) then out=x + y else out = x & ynoif (no) then out = !out
These 6 control bits work one after another (按顺序进行操作).
比如zx 和 nx都是 “0”,那么就是让x不做任何操作,保持原样。
如果zx 是 nx都是 “1”,那么就是先转为 “0”,再取反,就是把x各位都转化为 “1”。
Some Questions
Q. How does this magically happened? It didn’t do the addition or subtraction as we learned earlier 0 0
A. We don’t want to get too much into it…
Q. 6 control bits can have $2^6 $ representations, why are there only 16 functions?
A. Try out some other combinations, you will find them produce nothing interesting.
Q. What are zr and ng designed for?
A. They are to say something about the main output out.
if (out == 0) then zr = 1 else zr = 0if (out < 0) then ng = 1 else ng = 0
Simplicity is the ultimate sophistication. ——Leonardo da Vinci