这一章除了复习了一遍以前学过的与非或逻辑门,还介绍了为什么一个与非门就能表示所有的逻辑表达式。
Boolean logic (unit 1.1 – 1.3)
Algebra rules
Commutative laws
- x AND y == y AND x
- x OR y == y OR x
Associative laws
- x AND (y AND z) == (x AND y) AND z
- x OR (y OR z) == (x OR y) OR z
Distributive laws
- x AND (y OR z) == (x AND y) OR (x AND z)
- x OR (y AND z) == (x OR y) AND (x OR z)
De Morgan laws
- NOT (x AND y) == NOT (x) OR NOT (y)
- NOT (x OR y) == NOT (x) AND NOT (y)
Other rules
- x AND x == x
- x OR x == x
Truth table to Boolean Expression
Focus all the “1” results
write down all the expressions which only apply to the single rows in the truth table
OR these expressions together
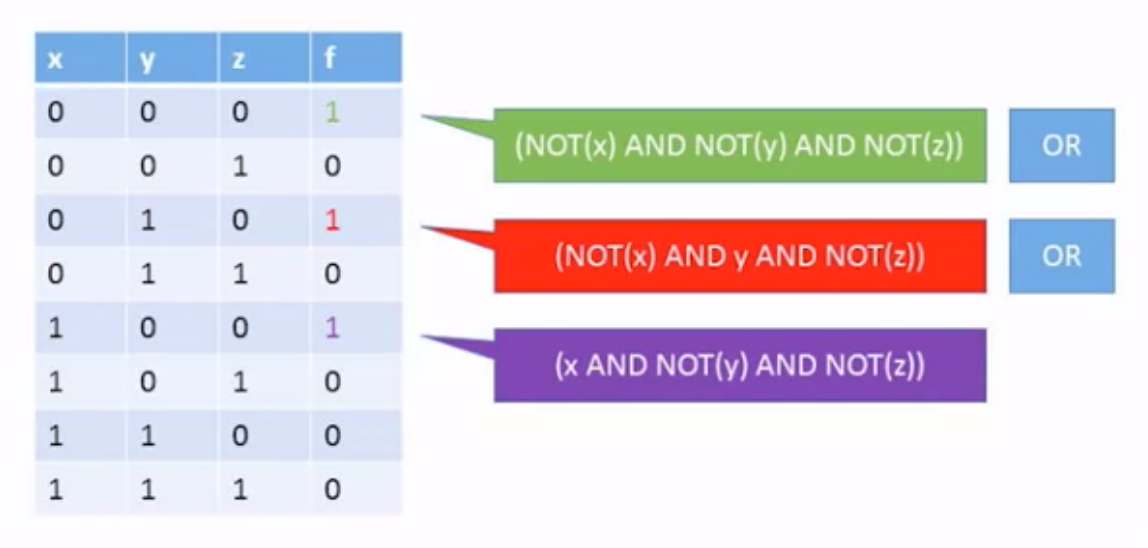
Simplify it.
In the example above, give a close look at the first two clauses: we have both possibilities for “y” and the same fixed value for “x”. So, we can combine the two clauses, which does not ask about y and only ask about “NOT(x)” and “NOT(z)”.
Then keep doing this.

Note that finding the shortest expressions is not easy for humans nor for algorithms, because this is a NP-hard problem.
To prove Why-Nand
The Theorem
Any Boolean function can be represented using an expression only containing AND and NOT operations.
Then, we introduce the NAND gate, which is proved to be the only needed gates.
Here comes the Nand
x NAND y == NOT (x AND y)
“NAND” is short for “NOT AND”.
Nand takes over.
- NOT (x) == x NAND x
- x AND y == NOT (x NAND y)
The gate interface in unique. There is only one way to describe its functionality. Meantime, there are multiple implementations that realize the same obstruction. This duality of “one obstruction, many different implementations” is very typical in Computer Science.
所以这里解答了我对计算机的一个疑问,那就是不必纠结一个复杂的功能最底层到底是怎么实现的,而是像这门课一样,分层地理解。了解了一层以后,就把这层的知识作为已知,再去了解上面一层。
补充一个后面答疑问到的几个关于Nand的问题:
Q. 用NAND以外别的gate做计算机的基础行不行?
A. 当然可以,比如NOR (NOT OR)。这就像物理中用不同的坐标系一样。只不过NAND相比于其他gate造价相对便宜。
Q. 这门课直接把Nand拿来用,但是黑盒里面是怎么实现的呢?
A. 这更像是一个物理问题,不属于这门课的范围。但是很容易举出一个实现的例子:用NMOS实现与非门电路